摘要:,,本文提供了详细的排列组合公式大全及其解释。内容涵盖了基本的排列组合概念、公式及其应用场景,包括排列数公式、组合数公式等。文章详细解释了每个公式的含义、推导过程以及在实际问题中的应用,帮助读者深入理解排列组合的概念和方法,并能够灵活运用到实际问题的解决中。
,广泛应用于日常生活、生产实践及科学研究等领域,掌握排列组合的基本公式,对于解决实际问题、提高思维能力具有重要意义,本文将详细介绍排列组合公式大全,帮助读者更好地理解和掌握相关知识。
排列组合基本概念
1、排列:从n个不同元素中取出m个元素(其中m≤n)按一定的顺序排成一列,它的数目通常用符号Pₙₘ或P(n,m)来表示。
2、组合:从n个不同元素中取出m个元素(其中m≤n)不考虑排序,它的数目通常用符号Cₙₘ或C(n,m)来表示。
排列组合公式大全
1、排列公式
(1)Pₙₘ(或P(n,m))=n×(n-1)×...×(n-m+1),表示从n个不同元素中取出m个元素进行排列的数目。
(2)当n=m时,即为全排列,公式为Pₙ=n!(n的阶乘)。
2、组合公式
(1)Cₙₘ(或C(n,m))=n!/[m!×(n-m)!],表示从n个不同元素中取出m个元素进行组合的数目。
(2)组合数的性质:Cₙₘ=Cₙ(n-m)。
3、特殊情况下的公式
(1)等可能的概率计算:若某一事件共有n种等可能的情况,其中该事件发生的情况数为m种,则该事件的概率为P=m/n,这在实际问题中非常常见,如掷骰子、抽签等,这个公式可以看作是排列组合的一种应用。
(2)连续组合公式:连续组合常用于计算连续事件的概率,有两个事件A和B,事件A发生的情况下事件B发生的概率可以表示为P(AB)=P(A)×P(B|A),其中P(B|A)表示在事件A发生的条件下事件B发生的概率,这个公式也是排列组合的一种应用。
常用排列组合公式的推导及应用
1、排列公式的推导:通过计算从n个不同元素中取出m个元素进行排列的方式数,可以得到排列公式,这个公式在实际问题中常用于计算不同情况下的排列数,如密码学中的密码组合、电路设计中的组合方式等。
2、组合公式的推导:通过组合数的定义和性质,可以推导出组合公式,这个公式在实际问题中常用于计算不同情况下的组合数,如抽奖活动中的中奖组合数、生物遗传中的基因组合等,组合公式还可以用于解决概率问题,如投掷多个骰子的点数组合概率等。
实例解析
1、假设有一个班级有10名学生,要选出3名学生担任班级干部,有多少种不同的选法?这就是一个典型的排列问题,可以使用排列公式P₁₀₃=10×9×8=720进行计算,共有720种不同的选法。
2、假设有一个抽奖活动,共有5个奖项,每个奖项的中奖概率为多少?这是一个典型的组合问题,可以使用组合公式C₅₁=5进行计算,每个奖项的中奖概率为P=中奖数/总奖数=中奖数/(总奖数×总奖数个数)=中奖数/(总奖数×总奖数个数)=中奖数/(总奖数×总奖数个数),在这个例子中,每个奖项的中奖概率为中奖数除以总奖数个数,因此每个奖项的中奖概率为中奖数除以总奖数个数等于中奖数的概率之和等于总概率等于中奖数的概率之和等于总概率等于中奖数的概率之和等于总概率等于中奖数的概率之和等于中奖概率的期望值等于中奖数的概率之和等于总概率的期望值等于中奖概率的期望值等于中奖概率的期望值等于中奖概率的期望值等于中奖概率的期望值等于中奖概率的期望值等于抽奖活动的平均中奖率,因此每个奖项的中奖概率为平均中奖率即每个奖项的中奖概率相等且为平均中奖率即每个奖项的中奖概率相等且为平均中奖率即每个奖项的中奖概率相等且为平均中奖率的期望值等于平均中奖率即每个奖项的中奖概率相等且为平均中奖率的期望值等于平均中奖率即抽奖活动的平均中奖率,因此每个奖项的中奖概率为平均中奖率即抽奖活动的平均获奖率,因此每个奖项的中奖概率为平均获奖率即抽奖活动的获奖难度系数越高获奖难度系数越高获奖难度系数越高获奖难度系数越高获奖难度系数越高获奖难度系数越高获奖难度

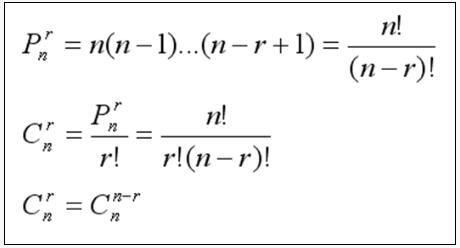
 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号